Density and dispersion are two descriptors of populations that can provide insight into processes such as competition and territoriality. Their measurement is therefore fundamental to our understanding of biogeography.
Populations have several characteristics that ecologists use to describe them. How individuals are arranged in space, or dispersion, informs us about environmental associations and social interactions among individuals in the population. How many organisms there are per unit area is referred to as density. Both of these characteristics can be measured in a variety of ways (Krebs 1999).
Density
Density can be estimated in a variety of different ways depending on the organism and habitat you are sampling. Quadrat sampling is one-way ecologists accomplish this. Quadrat sampling involves deciding what size and shape of area you will sample and deciding how many samples to take. Many studies use the literature as a guide to the size and shape of quadrats that can be used. It is also plausible to determine what quadrat size and shape are optimal for the study you wish to conduct (Krebs, 1999). This type of method can be problematic if the organisms you are studying are at low densities and/or occur in clumps across the landscape. Quadrat methods can also be used to extrapolate densities from indirect measures (e.g., animal droppings, tracks, nests).
Although quadrat sampling is simple and widely used, for some organisms it is not appropriate. Thus, many other types of methods have been developed. For many animal populations, mark-recapture methods are utilized where individuals are caught, marked, released and then another sample taken. The proportion of marked individuals can then be used to estimate the total population size. This is called the Peterson method and is the simplest of the many mark-recapture methods available to ecologists (Krebs 1999). For animals or plants that are sedentary or can be identified and located before they move, plotless methods, like the line-intercept method, can be applied (Krebs 1999).
The density of organisms varies depending on a variety of factors. Deaths, births, immigration, and emigration are all processes that can impact population density at a given time. However, there are general trends associated with density. For example, across a number of species, smaller organisms tend to occur at higher densities than larger organisms (White et al. 2007, Lewis et al. 2008, Rossberg et al. 2008). Although our understanding of these processes and patterns associated with density has improved, there is still an enormous amount of descriptive and experimental work needed to understand how organismal characteristics are associated with density (Blackburn et al. 2006).
Dispersion
Patterns of Dispersion
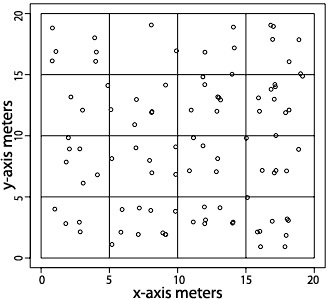
How individuals are arranged in space can tell you a great deal about their ecology. For instance, Figure 1 shows the distribution of a hypothetical species. Most people would describe this as a random pattern in space. However, if you look closely you will notice that individuals are not actually randomly distributed, they are maintaining a fairly uniform distance between each other. Why do you think that is? Figure 2 shows the distribution of another hypothetical species. This time they are grouped together in certain 5 x 5 meter areas but not in others. What might this tell you about this species and its interactions with the environment? Figure 3 shows the distribution of individuals of a hypothetical species that is actually random. One thing that you'll notice is that it is difficult to think of this as random!

These three figures illustrate the three different patterns of dispersion that ecologists observe. Clumped dispersion (Figure 1) where individuals are aggregated in certain areas of the sampled space. Uniform dispersion (Figure 2), where individuals are almost equally spaced apart from each other and random dispersion (Figure 3).

Behavioral and ecological factors influence dispersion. Uniform patterns of dispersion are generally a result of interactions between individuals like competition and territoriality. Clumped patterns usually occur when resources are concentrated in small areas within a larger habitat or because of individuals forming social groups. At large spatial scales most organisms appear to have clumped distributions because their habitats are not uniformly distributed over wide areas. Although you might not think of plants as territorial, they too can have uniform dispersion patterns that are a result of territoriality and competition (e.g., shading, allelopathy, and root interactions; Mahall & Callaway 1992, Schenk et al. 1999). Random dispersion patterns are atypical in nature and could indicate a uniform or random distribution of resources or a lack of interactions among individuals in the population.
Which Dispersion Pattern is it?
Humans are not always very good at distinguishing among the different patterns of dispersion, so statistical methods are usually used to tell the difference between them.
A very simple method that can be used to determine dispersion patterns is based on the sample mean and variance of the number of individuals counted in repeated quadrats in a particular area that is sampled. The sample mean is the average collected from the sample. As an example, let's examine Figure 1. This figure is divided into squares, and each square represents a sample of organisms in space. In this case the organisms are clumped in space and there are 4 samples with 25 organisms and 12 with no organisms. The sample mean is calculated as the sum of all of the observations (25 + 25 + 25 + 25 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0) divided by the total number of samples (16). Thus the mean number per square in Figure 1 is 6.25. The variance is calculated by squaring the differences between the sample mean and each of the observations, adding them up to produce the sum of the squares, and dividing by the sample size minus 1. So the variance in this case would be ([25 - 6.25]2 + [25 - 6.25]2 + [25 - 6.25]2 + [25-6.25]2 + [0 - 6.25]2 + [0 - 6.25]2 + [0 - 6.25]2 + [0 - 6.25]2 + [0 - 6.25]2 + [0 - 6.25]2 + [0-6.25]2 + [0 - 6.25]2 + [0 - 6.25]2 + [0 - 6.25]2 + [0 - 6.25]2)/(16 - 1) which is 125. So in Figure 1 the average number of individuals per grid square is 6.25 and the variance among grid squares is 125. The ratio of the variance to the mean can then be used to determine whether the pattern is uniform or clumped, and is referred to as the index of dispersion (Krebs 1999). In this case the ratio is 20, which is much greater than 1! This indicates that individuals in this population are exhibiting a clumped spacing pattern in the sampled habitat. If this ratio is less than one, it indicates a uniform distribution (e.g., Figure 2, ratio = 0.427). Whereas if it is one, that indicates individuals are randomly distributed in space (e.g., Figure 3, ratio = 0.841). While this method is extraordinarily simple and widely illustrated in many texts, it can potentially fail to detect some non-random patterns of dispersion (see Krebs 1999).
The distances between individuals can also be used to determine dispersion patterns. Several indices exist, but all operate using similar principles. If individuals are aggregated or clumped (Figure 2), their nearest neighbor will be much closer than you would expect if individuals were randomly distributed in space (Figure 3). If they were uniformly distributed (Figure 1), on average, you would predict individuals to be further apart than would be expected if they were randomly distributed.
A Case Study: Dispersion Patterns in Spiders

Explaining these patterns requires investigation of the availability of suitable habitat as well as the interactions among individuals. At a larger spatial scale a very small amount of the habitat is suitable for websites and, of course, that is where the spiders are (Riechert 1981). These spiders prefer large depressions in grassland habitats with characteristics attractive to insect prey (e.g., flowering shrubs, the presence of litter, and animal feces) and have favorable thermal properties (Reichert & Gillespie 1986). The spatial distribution of these suitable habitats is what generates the clumped pattern at a larger scale. Since high quality websites are limited in the habitat, and the presence of other spiders in close proximity reduces the fitness of the resident spider, residents will actively patrol their website and engage in aggressive behavior towards other spiders enter into their territory (Riechert 1981). These interactions generate a minimum spacing among individuals within suitable habitat patches, and the occasional displacement of individuals from their website (Riechert 1981, Riechert & Gillespie 1986). Aggressive interactions like these are typical of the types of behavioral interactions that generate uniform spacing patterns.


ConversionConversion EmoticonEmoticon